SF (FX-603P)
Table of Contents

Description #
Calculates the Superformula for any angle Φ from Φ = 0 degree to Φ = 359 degrees.
\begin{equation} r(\phi) = \frac{1}{ \sqrt[n₁]{ \left| \frac{ \cos \left(\frac{m \phi}{4} \right) }{a} \right|^{n₂} + \left| \frac{ \sin \left(\frac{m \phi}{4} \right) }{b} \right|^{n₃} } } \end{equation}
| Variable | Effect |
|---|---|
| m | edges of shape |
| n₁ | resizes the spikes of the shape |
| n₂ | defines shape |
| n₃ | defines shape |
| a | resize cos aspect of shape |
| b | resize sin aspect of shape |
| Φ | angle from 0 … 360 (0 … 2π) |
| r | resulting distance from orgin |
Note: If A and B are different then the shape might not form a closed loop.
Sample input #
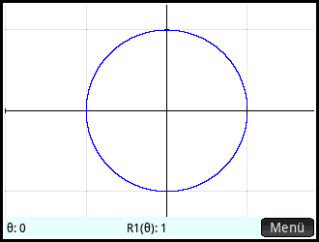
Circle #
Using these values the Superformula should give a figure looking like a circle: \(a=1;\ b=1;\ n_1=2;\ n_2=2;\ n_3=2;\ m=2 \).
How the code works #
For quick input the values for n₁, n₂, n₃ and m are pre-set with value 2 but can instead be overwritten if different.
Then in P0 the angle is set to 0 degree and is incremented by 1 at the ending
of the program.
To obtain a full circle the Memory Register 06 (MR06) is set to the end
value “359”. (In run mode MR06 is actually to enter to recall the memory
register for register 06.)
Sample output #
The program generated coordinate pairs, as pasted and copied out of the printer simulation:
+X= +Y=
1.0000 0.0000
1.0000 0.0175
0.9994 0.0349
0.9986 0.0523
0.9976 0.0698
…
0.0698 0.9976
0.0523 0.9986
0.0349 0.9994
0.0175 1.0000
0.0000 1.0000
-0.0175 1.0000
-0.0349 0.9994
-0.0523 0.9986
-0.0698 0.9976
-0.0872 0.9962
…
-0.9976 0.0698
-0.9986 0.0523
-0.9994 0.0349
-1.0000 0.0175
-1.0000 0.0000
-1.0000 -0.0175
-0.9994 -0.0349
-0.9986 -0.0523
-0.9976 -0.0698
-0.9962 -0.0872
…
-0.0872 -0.9962
-0.0698 -0.9976
-0.0523 -0.9986
-0.0349 -0.9994
-0.0175 -1.0000
0.0000 -1.0000
0.0175 -1.0000
0.0349 -0.9994
0.0523 -0.9986
0.0698 -0.9976
…
0.9945 -0.1045
0.9962 -0.0872
0.9976 -0.0698
0.9986 -0.0523
0.9994 -0.0349
1.0000 -0.0175
End.
Note: Values are rounded to 4 digits.
Interpretation #
Here the angle Φ runs through a full rotation if register MR06 is set to the
value 360.
Program #
The program file contains the one programs P0 that looks like this:
All Program List
P0
MAC 0 Min0F 360 Min06 "N1?" 2 HLT
Min01 "N2?" 2 HLT
Min02 "N3?" 2 HLT
Min03 "M?" 2 HLT
Min04 1 Min08 1 Min09 "+X= +Y=" PRT FEXE
LBL0 MR0F * MR04 / 4 = Min05 COS / MR08
= ABS X^Y MR02 = Min07 MR05 SIN / MR09 =
ABS X^Y MR03 = M+07 MR07 X^(1/Y) MR01
1/X P>R MR0F = FIX4 " #" X<>Y FIX4 "; #"
PRT FEXE
1 M+0F MR06 X=F GOTO1
GOTO0
LBL1 "End." PRT FEXE
END
Memory registers #
While using the same variable names as in the Wikipedia article, the memory registers are set as follows:
| Memory | Content |
|---|---|
| M01 | n₁ |
| M02 | n₂ |
| M03 | n₃ |
| M04 | m |
| M05 | \( \frac{m \phi}{4} \) |
| M06 | 360 |
| M07 | r |
| M08 | a |
| M09 | b |
| M0F | Φ |
To the developer #
The display cannot hold both coordinates at the same time that the values are scrolled through which is very time consuming.
I suggest you to code a switch in the simulator for allowing to turn off the display of to be printed values, while the display can show a counter value instead.
Author #
Michael Malien, Facebook