SF (FX-602P)
Table of Contents

Description #
Calculates the Superformula for any angle Φ from Φ = 0 degree to Φ = 359 degrees.
\begin{equation} r(\phi) = \frac{1}{ \sqrt[n₁]{ \left| \frac{ \cos \left(\frac{m \phi}{4} \right) }{a} \right|^{n₂} + \left| \frac{ \sin \left(\frac{m \phi}{4} \right) }{b} \right|^{n₃} } } \end{equation}
| Variable | Effect |
|---|---|
| m | edges of shape |
| n₁ | resizes the spikes of the shape |
| n₂ | defines shape |
| n₃ | defines shape |
| a | resize cos aspect of shape |
| b | resize sin aspect of shape |
| Φ | angle from 0 … 360 (0 … 2π) |
| r | resulting distance from orgin |
Note: If A and B are different then the shape might not form a closed loop.
Sample input #
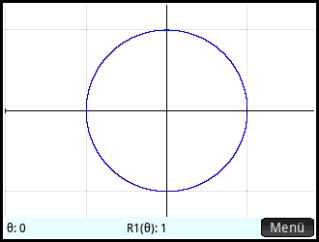
Circle #
Using these values the Superformula should give a figure looking like a circle: \(a=1;\ b=1;\ n_1=2;\ n_2=2;\ n_3=2;
m=2 \).
How the code works #
For quick input the values for n₁, n₂, n₃ and m are pre-set with value 2 but can instead be overwritten if different.
Then in P0 the angle is set to 0 degree and is incremented by 1 at the ending of the program.
To obtain a full circle the Memory Register 06 (MR06) is set to the end value “359”. (In run mode MR06 is actually
to enter to recall the memory register for register 06.)
Sample output #
The program generated coordinate pairs, as pasted and copied out of the printer simulation:
+X= +Y=
1.0000 0.0000
1.0000 0.0175
0.9994 0.0349
0.9986 0.0523
0.9976 0.0698
…
0.0698 0.9976
0.0523 0.9986
0.0349 0.9994
0.0175 1.0000
0.0000 1.0000
-0.0175 1.0000
-0.0349 0.9994
-0.0523 0.9986
-0.0698 0.9976
-0.0872 0.9962
…
-0.9976 0.0698
-0.9986 0.0523
-0.9994 0.0349
-1.0000 0.0175
-1.0000 0.0000
-1.0000 -0.0175
-0.9994 -0.0349
-0.9986 -0.0523
-0.9976 -0.0698
-0.9962 -0.0872
…
-0.0872 -0.9962
-0.0698 -0.9976
-0.0523 -0.9986
-0.0349 -0.9994
-0.0175 -1.0000
0.0000 -1.0000
0.0175 -1.0000
0.0349 -0.9994
0.0523 -0.9986
0.0698 -0.9976
…
0.9945 -0.1045
0.9962 -0.0872
0.9976 -0.0698
0.9986 -0.0523
0.9994 -0.0349
1.0000 -0.0175
End.
Interpretation #
Here the angle Φ runs through a full rotation if register MR06 is set to the
value 360.
Program #
The program file contains the one programs P0 that looks like this:
SF2.pf #
PROGRAM LIST
File : SF2
*** P0
MAC 0 Min0F 360
Min06 “N1?” PAUSE 2
HLT Min01 “N2?”
PAUSE 2 HLT Min02 “N
3?” PAUSE 2 HLT
Min03 “M?” PAUSE 2
HLT Min04 1 Min08 1
Min09 “+X= +Y=”
SAVE invEXE
LBL0
MR0F × MR04 ÷ 4 =
Min05 cos ÷ MR08 =
abs X^y MR02 = Min07
MR05 sin ÷ MR09 =
abs X^y MR03 = M+07
MR07 X^⅟y MR01 1/x =
P→R MR0F = FIX4 “ #”
X↔Y FIX4 “; #” SAVE
invEXE 1 M+0F MR06
x=F GOTO1
GOTO0
LBL1
“End.” SAVE invEXE
···127 steps
Memory registers #
While using the same variable names as in the Wikipedia article, the memory registers are set as follows:
| Memory | Content |
|---|---|
| M01 | n₁ |
| M02 | n₂ |
| M03 | n₃ |
| M04 | m |
| M05 | \( \frac{m \phi}{4} \) |
| M06 | 360 |
| M07 | r |
| M08 | a |
| M09 | b |
| M0F | Φ |
To the developer #
The display cannot hold both coordinates at the same time that the values are scrolled through which is very time consuming.
I suggest you to code a switch in the simulator for allowing to turn off the display of to be printed values, while the display can show a counter value instead.
Author #
Michael Malien, Facebook